一、引题
在一个N行M列的二维数组vec,每个元素位置放置一定数量的苹果,从底部开始往顶部走,每一步只能按 正前方、正前方左45度(如果左边还有位置)、正前方右45度(如果右边还有位置) 三种方式前进,起点可以是底部的任意一个位置,终点也可以是顶部的任意一个位置,求一条路径,使得按这条路径走过时能收集到最多的苹果。
分析
结果是要找出一条路径,使得按这条路径走时能收集到最多的苹果,这是找最优结果的问题。这样的路径当然没法一眼就看出来,可以随便画一条路径,但没法证明这条路径能得出最优结果。
那么能不能假设一个点vec[i][j],这个点是最优路径上的一个点。尽管现在还不能证明vec[i][j]肯定处于最优路径上,但我们就是假设它是(这是动态规划的分析的一个特点)!
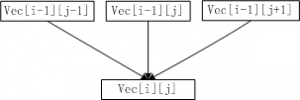
用cc[i][j]表示达到点vec[i][j]时能收集到的最多苹果数。按照题目的要求,如果vec[i][j]不是处于最底行,那么到达vec[i][j]最多有三种走法:
- 如果左上方还有位置,从vec[i-1][j-1]向右前方前进一步。
- 从vec[i-1][j]按正前方前进一步。
- 如果右上方还有位置,从vec[i-1][j+1]向左前方前进一步。
要在vec[i][j]收集到最多苹果,当然是从它的三个来源中选一个能收集到最多苹果的节点作为vec[i][j]在最优路径上的前一个节点。那么在vec[i][j]上收集到的苹果数为:
cc[i][j] = vec[i][j] + max{ cc[i-1][j-1] if j-1>=0, cc[i-1][j], cc[i-1][j+1] if j+1 < M } if i-1 >= 0
现在虽然知道怎么求cc[i][j]的公式,但cc[i-1][j-1] , cc[i-1][j], cc[i-1][j+1]的值现在都还不知道,需要继续求解。在求cc[i-1][j-1]时,并不需要去管 >=i 的行,只需要关注第 i-2行,所以,问题的规模缩小了。
同样对于节点vec[i-1][j-1],如果它不是处于最底行,它也最多有三个来源,它的位置能收集到的最多苹果数也是它的三个来源中能收集到的最多苹果数加上它自身的苹果数。所以求节点能收集到的最多苹果数具有递归的性质。
递归总得有个终止条件,这里的终止条件就是处于最底行的节点,因为移动的方向只能向前,不能左右移动,所以最底行能收集到的最多苹果数就是本身持有的苹果数。
到这里,我们可以用递归的方法求出任一节点vec[i][j]所能收集到的最多苹果数cc[i][j]。
再来看看这种情况:对于节点 vec[i][j]和vec[i][j+1],它们都可以从vec[i-1][j]到达,如果用递归的方法求解的话,那么会重复求解cc[i-1][j]的值,这是低效的。
如果我们先求出cc[i-1][j]的值,那么在求解vec[i][j]和vec[i][j+1]时,由于cc[i-1][j]已经求解过,就不需要再重复计算了。
如果只需要计算能收集的最大苹果数,直接从cc表的最顶行取最大值即可;如果需要计算完整的路径,那么还需要用另一个表route来记录节点vec[i][j]选择的来源节点。
小结
如果把求某个节点能收集的最大苹果数看作是一个问题,那么求解它的来源节点能收集的最大苹果数就是它的子问题了。
- 虽然不知道最终结果,但可以大胆假设某个点就是最优路径上的一个节点。
- 当前节点能收集的最大苹果数是从它的多个来源节点中选择能收集到最多苹果的节点。也就是当前问题的最优解包括从它的多个子问题中选最优的一个子问题的解。
- 自顶向下地分析所有节点能收集到的最多苹果数,直至遇到终止条件(最底行)。
- 分析发现,虽然用自顶向下的递归方法可以求解问题,但会导致重复计算子问题。
- 自底向上计算问题的最优解,并把得到的解存在表格里,可以避免重复计算子问题。
实现
实现不难,就不贴代码了。
二、动态规划
引题的分析过程就是应用动态规划方法的分析过程,下面的内容主要来自《算法导论》第3版,更理论的。
动态规划通常应用于最优化问题。
动态规划算法的设计步骤
- 描述最优解的结构。(通过剪贴技术证明有最优解)
- 递归定义最优解的值。(得出计算值的递归式)
- 按自底向上的方式计算最优解的值。
- 由计算出的结果构造一个最优解。
适合采用动态规划方法的最优化问题中有两个要素:最优子结构和重叠子问题。
最优子结构
如果问题的一个最优解中包含了子问题的最优解,则该问题具有最优子结构。
在寻找最优子结构时,可以遵循一种共同的模式:
- 问题的一个解可以是做一个选择。
- 假设对一个给定的问题,已知的是一个可以导致最优解的选择。不必关心如何确定这个选择,尽管假定它是已知的。
- 在已知这个选择后,要确定哪些子问题会随之发生,以及如何最好地描述所得到的子问题空间。
- 利用一种“剪贴”(cut-and-paste)技术,来证明在问题的一个最优解中,使用的子问题的解本身也必须是最优的。通过假设每一个子问题的解都不是最优解,然后导出矛盾,即可做到这一点。
剪贴技术大致是这样的:对于一个问题P,有子问题C1、C2、C3,假设P的最优解包含C1的最优解,如果C3的最优解比C1的最优解还好,那么把C1的最优解从P的解剪切下来,再把C3的的最优解粘贴到P的最优解上,可以得到一个更好的解,与原有假设矛盾,所以P的最优解应该是包含子问题C3的最优解。
最优子结构在问题域中以两种方式变化:
- 有多少个子问题被使用在原问题的一个最优解中,以及
- 在决定一个最优解中使用哪些子问题时有多少个选择。
同一个问题的子问题之间应该是独立的,一个子问题的解不会影响同一个问题中另一个子问题的解。
重叠子问题
适用于动态规划求解的最优化问题必须具有的第二个要素是子问题的空间要“很小”,也就是用来解原问题的递归算法可反复地解同样的子问题,而不是总在产生新的子问题。
动态规划算法总是充分利用重叠子问题,即通过每个子问题只解一次,把解保存在一个需要时就可以查看的表中,而每次查表的时间为常数。
子问题独立性和重叠性
动态规划要求其子问题既要独立又要重叠,这其实是不同的概念。
独立性是从兄弟节点之间的角度来看,是同一问题下的子问题之间独立。
重叠性是从父子节点之间的角度看,一个问题p和p的子问题t,他们共有子子问题c,即t的子问题c也是p的子问题,那么求解出问题t后,求解问题p时,由于它的一个子子问题c已经求出,可以重用,所以只需计算一部分子问题,从而提高效率。
三、动态规划与分治法的异同
动态规划和分治法一样,都是通过组合子问题的解而解决整个问题。
分治法是指将问题划分成一些独立的子问题,递归地求解各子问题,然后合并子问题的解而得到原问题的解。
动态规划适用于 子问题不是独立的情况,也就是各子问题包含公共的子子问题。
在这种情况下,若采用分治法则会做许多不必要的工作,即重复地求解公共的子子问题。
动态规划算法对每个子子问题只求解一次,将其结果保存在一张表中,从而避免每次遇到各个子问题时重新计算答案。
四、最长公共子序列
这里结合前面的理论的知识再练习下动态规划的解题过程。
最长公共子序列,Longest-Common-Subsequence,LCS。
给定两个序列X和Y,如果Z既是X的一个子序列又是Y的一个子序列,则称序列Z是X和Y的公共子序列。
例如,X=< A, B, C, B, D, A, B>, Y=< B, D, C, A, B, A>,< B, C, A>是X、Y的一个公共子序列,但不是最长的;序列< B, C, B, A>、< B, D, A, B>才是X、Y的LCS。
那么对于给定的两个序列X、Y,怎么求他们的最长公共子序列?
分析
既然是要求最长的公共子序列,就是要求问题的最优解,听起来正是动态规划的菜。
下面尝试按动态规划算法的步骤求解问题:
-
步骤1、描述最优子结构,在这里就是要描述一个最长公共子序列。
设X[1,..,m]和Y[1,..,n]为两个序列,并假设Z[1,..,k]为X和Y的任意一个LCS(大胆假设,怎么得到先不管)。LCS定理:
- 如果
X[m]=Y[n],那么Z[k]=X[m]=Y[n], 而且Z[k-1]是X[1,...,m-1]和Y[1,...,n-1]的一个LCS。 - 如果
X[m]!=Y[n],那么Z[k]!=X[m](排除X[m]),蕴含Z是X[1,...,m-1] 和Y` 的一个LCS。 - 如果
X[m]!=Y[n],那么Z[k]!=Y[n](排除Y[n]),蕴含Z是X和Y[1,...,n-1]的一个LCS。
证明:
- 如果
Z[k]!=X[m],则可以添加X[m]=Y[n]到Z中,以得到X和Y的一个长度为k+1的公共子序列,这与Z是X和Y的最长公共子序列的假设矛盾。因此,必有Z[k]=X[m]=Y[n]。此时前缀Z[k-1]是X[1,...,m-1]和Y[1,...,n-1]的长度为k-1的公共序列。证明它就是LCS,为导出矛盾,假设X[1,...,m-1]和Y[1,...,n-1]有一个长度大于k-1的公共子序列W,用剪贴技术:将原有前缀Z[k-1]从Z上剪切下来,再把W粘贴到Z上,则可以得到一个比k大的公共子序列,与原有假设矛盾,所以Z[k-1]就是X[1,...,m-1]和Y[1,...,n-1]的LCS。 - 如果
Z[k]!=X[m],那么Z是X[1,...,m-1]和Y的一个公共子序列。如果X[1,...,m-1]和Y有一个长度大于k的公共子序列W,则W也是X[m]和Y的一个公共子序列,这与Z是X和Y的一个LCS的假设矛盾。 - 与2同理可证。
小结:LCS定理说明两个序列的一个LCS也包含了两个序列的前缀的一个LCS,也就是说LCS问题具有最优子结构性质。
- 如果
-
步骤2、递归解。
在找X[1,..,m]和Y[1,..,n]的一个LCS时,如果X[m]=Y[n],必须找出X[1,...,m-1]和Y[1,...,n-1]的一个LCS,再将X[m]=Y[n]添加到这个LCS上,产生X和Y的一个LCS。如果X[m]!=Y[n],必须解两个子问题X[1,...,m-1]和Y[1,..,n]的一个LCS,以及X[1,..,m]和Y[1,...,n-1]的一个LCS,这两个LCS中较长的就是X[1,..,m]和Y[1,..,n]的LCS。
所以为找出X[1,..,m]和Y[1,..,n]的LCS,必然需要找X[1,...,m-1]和Y[1,...,n-1]的LCS的子子问题。因此,LCS具有重叠子问题的性质。由前面的推理过程可得递归式:
lcs[i,j] = 0, if i=0 || j=0 lcs[i-1][j-1]+1, if i,j>0 && X[i]=Y[j] max(lcs[i,j-1], lcs[i-1][j]) if i,j>0 && X[i]!=Y[j] -
步骤3、自底向上计算最优解。
除了用一个表来保存计算得到的最优解,一般还需要另一个表来记录在多个子问题之间所做出的选择,代码大致如下:for i := 1; i < row; i++ { for j := 1; j < col; j++ { if X[i-1] == Y[j-1] { lcs[i][j] = lcs[i-1][j-1] + 1 selection[i][j] = '\\' } else { max := lcs[i-1][j] selection[i][j] = '|' if max < lcs[i][j-1] { max = lcs[i][j-1] selection[i][j] = '-' } lcs[i][j] = max } } } -
步骤4、构建最优解,这里就输出一个LCS:代码大致如下:
func printLCS(selection [][]int, X []int, i, j int) { if i == 0 || j == 0 { return } else if selection[i][j] == '\\' { printLCS(selection, X, i-1, j-1) fmt.Printf("%c ", X[i-1]) } else if selection[i][j] == '|' { printLCS(selection, X, i-1, j) } else { printLCS(selection, X, i, j-1) } }
这就是用动态规划法解题的完整过程,包括了一些证明过程。
五、一些练习题
-
一个序列有N个数:
A[1],A[2],…,A[N],求出最长非降子序列的长度。对于序列5,3,4,8,6,7,3, 4, 6, 7就是其中一个最长非降子序列。 -
如果我们有面值为1元、3元和5元的硬币若干枚,如何用最少的硬币凑够11元?
欢迎关注我的微信公众号: coderbee笔记,可以更及时回复你的讨论。