一个 8×8 的棋盘，希望往里放 8 个棋子，每个棋所在的行、列、对角线上都不能有其他棋子。找出所有满足要求的布局。
首先画出下面这样一个棋盘：
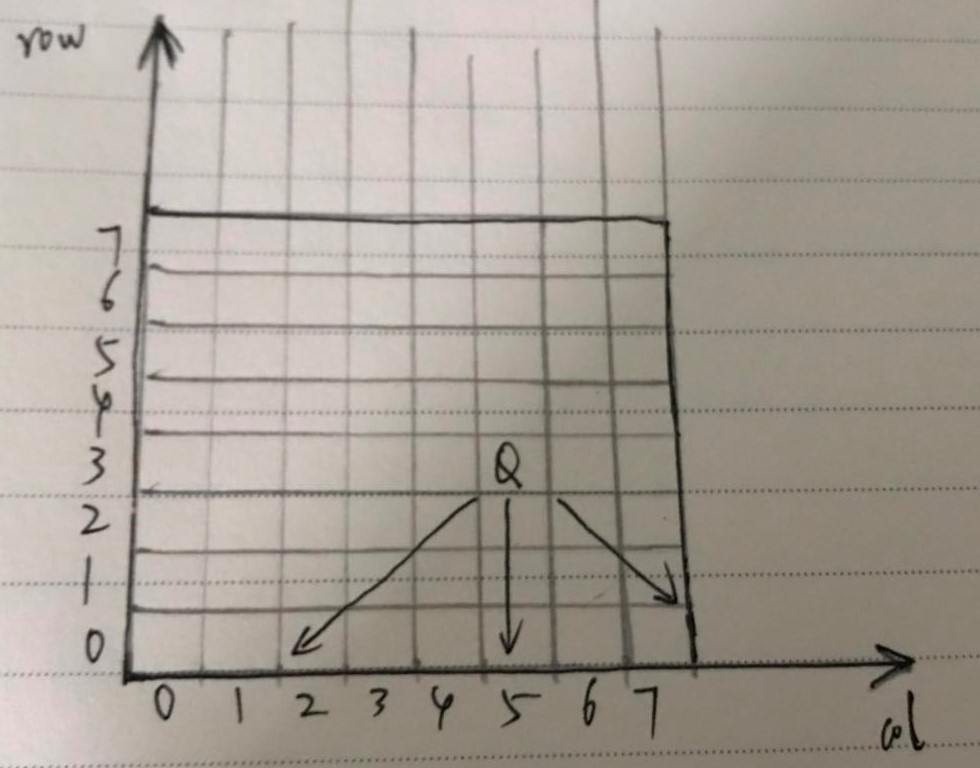
行、列的下标都是从 0 开始。
逐行摆放棋子，比如当前要摆放第 R 行的棋子时，认为 0 至 R-1 行的棋子是符合要求的，那么对于第 R 行，尝试把棋子摆放到第 C 列，检测是否满足要求，如果满足则继续下一行摆放下一行，不满足则则尝试放至 C+1 列。如果摆放到了第 8 行，则认为得到了一个解。
检测算法：从上图可以看出，只需要检查三种场景，对于位置(row, col)：
col >= 0 && (row--, col--)。col < 8 && (row--, col++)。散列一般也叫哈希。散列表也叫哈希表。本位将介绍散列表的基本知识、一致性哈希、哈希碰撞攻击及Java里的哈希实现。
散列表是普通数组概念的推广，在最坏情况下查找一个元素需要O(n)，在一些合理假设下，查找一个元素的期望时间为O(1)。
在散列表中，不是直接把关键字用作数组下标，而是根据关键字计算出下标。
散列函数：作用就是根据关键字计算出数组下标。
碰撞（collision）：多个关键字映射到同一个数组下标位置。
槽：一般把散列表的数组的一个存储单元（元素）叫做槽。
简单一致性散列：（Simple uniform hashing）假设任何元素散列到m个槽中的每一个的可能性是相同的，且与其他元素已被散列到什么位置上独立无关，这个假设称为简单一致性散列。
在一个N行M列的二维数组vec，每个元素位置放置一定数量的苹果，从底部开始往顶部走，每一步只能按 正前方、正前方左45度（如果左边还有位置）、正前方右45度（如果右边还有位置） 三种方式前进，起点可以是底部的任意一个位置，终点也可以是顶部的任意一个位置，求一条路径，使得按这条路径走过时能收集到最多的苹果。
结果是要找出一条路径，使得按这条路径走时能收集到最多的苹果，这是找最优结果的问题。这样的路径当然没法一眼就看出来，可以随便画一条路径，但没法证明这条路径能得出最优结果。
那么能不能假设一个点vec[i][j]，这个点是最优路径上的一个点。尽管现在还不能证明vec[i][j]肯定处于最优路径上，但我们就是假设它是（这是动态规划的分析的一个特点）！
用cc[i][j]表示达到点vec[i][j]时能收集到的最多苹果数。按照题目的要求，如果vec[i][j]不是处于最底行，那么到达vec[i][j]最多有三种走法：
图示：
要在vec[i][j]收集到最多苹果，当然是从它的三个来源中选一个能收集到最多苹果的节点作为vec[i][j]在最优路径上的前一个节点。那么在vec[i][j]上收集到的苹果数为：
cc[i][j] = vec[i][j] + max{ cc[i-1][j-1] if j-1>=0, cc[i-1][j], cc[i-1][j+1] if j+1 < M } if i-1 >= 0
题目均来自《编程珠玑》。
将一个n元一维向量向左旋转（循环移位）i个位置。例如，当n=8时且i=3时，向量abcdefgh旋转为defghabc。简单的代码使用一个n元的中间向量在n步内完成该工作。能否仅用数十个额外直接的存储空间，在正比于n的时间内完成向量的旋转？
旋转操作对应于交换相邻的不同大小的内存块：每当拖动文件中的一块文件到其他地方时，就要求程序交换两块内存中的内容。
方法一：首先将 x 的前 i 个元素复制到一个临时数组中，然后将余下的 n-i 个元素向左移动 i 个位置，最好将最初的 i 个元素从临时数组中复制到 x 中余下的位置。这种办法使用 i 个额外的位置产生了过大的存储空间的消耗。
方法二：定义一个函数将 i 向左旋转一个位置（其时间正比于 n），然后调用该函数 i 次。该方法产生了过多的运行时间消耗。
下面介绍三种更好的方法。
写出一个O(n)时间的非递归过程，输出给定的含n个节点的二叉树中每个结点的关键字，要求只能使用除树本身以外固定量的额外存储空间，而且在过程中不能修改该树，哪怕只是暂时的。
树的遍历可以分为广度优先和深度优先两种形式。
树的遍历可以分为先根遍历、中序遍历、后序遍历。前中后是以父节点在遍历中的顺序为根据的。
由于只能使用固定量的额外存储空间，所以，没法构建队列或栈来进行遍历 或 用变量标记哪些结点是已输出的。由于不能修改树，也没法在树上做标记。所以，结点是否已输出只能在遍历过程中判断，也就需要遍历的算法能够区分出已输出和未输出的。
如果采用广度优先的方式，先输出父结点后，由于没有足够的空间来存储对子树的引用，树可以说是变为两棵独立的树，这个方式应该是不可行的。
如果采用深度优先的方式，以中序遍历为例，总是按左子树、父结点、右子树的顺序遍历，那么当右子树遍历完后，说明父结点及其所有子树都遍历完成了，可以这样往上处理父结点的父结点。而判断右子树是否遍历完成可以通过：当前遍历完成的结点是否是父结点的右结点来完成。这种方法是可行的。
当结点p及其子树都遍历完成后，需要向上查找第一个未遍历的右子树（parent = p.parent）：
p == parent.rChild，当前遍历是子树是右子树，需要继续往上查找；编程计算给定的整数在用二进制来表示时含有多少个 1。
假定以高位在前、低位在后的形式，一个整数的二进制表示为：000110100；当该整数减1时，由于低位是0，所以会一直往高位借位，直至碰到最低位的1（竖线后面的那个1）：000110|100；减1之后整数那个最低位1变为0，之后的位都变为1：000110|011；此时进行 i & (i-1) 就会让竖线后面的都变为0：
000110|100 i
000110|011 i-1
000110|000 i&(i-1)
1110 -2
1101 -2 - 1
1100 -2 & (-2 - 1)
所以 i = i & (i-1) 都会让 i 里的位为 1 的个数减一。对于负数，同样具有这样的性质。
继续阅读
这里的堆不是编程语言里的堆，是一种数据结构。
堆像一棵倒立的满二叉树，每个节点最多有两个直接子节点。最上面的节点称为根节点，没有子节点的节点称为叶子节点，有子节点的节点称为分支节点。
堆有大顶堆和小顶堆之分。大顶堆是指分支节点大于它的所有子节点，堆里最大元素是根节点；小顶堆是指分支节点小于它的所有子节点，堆里最小元素是根节点。
堆排序是借助堆数据结构进行排序的一种高效算法，它的平均时间复杂度是O(n*lg(n))。
堆排序的核心是构建和维持堆。
实现时要注意的是：
以数组第一个节点（序号为0）为根，方便计算叶子节点。
大多数算法介绍都是以1为数组的起始下标的，左右叶子节点的计算分别为：lchild=2*parent; rchild =2*parent+1；而实际编程语言大多数都是以0为起始下标的，所以子节点计算需要调整为：lchild=2*parent+1; rchild=2*parent+2；因为根节点是0，导致根节点的左子树与根节点相同而出错。
构建是从底向上逐层构建堆，从最后一层的分支节点（ len(arr)/2 ）开始构建堆。
从堆顶取出最大元素与最后一个堆元素交互后，堆的大小减1。所以堆在排序过程中是逐渐缩小的，但根总是第一个元素，所以可以利用之前也构建好的堆，只需要调整一棵子树。
继续阅读
快速排序也是基于分治模式的，对于规模为n的数组，最坏情况运行时间是O(n^2)，平均运行时间是O(lg(n))。
对数组A[p…r]排序的分治过程的三个步骤：
从上面的步骤可以看到，快速排序的关键在划分子数组，且每次划分都产生一个元素，它所在的位置就是它最终的位置。
继续阅读
对于一个给定的整数数组arr[0...n)，求这样一个子数组，它的元素的累加和在所有子数组中是最大的。
这个题在《编程珠玑》一书中有介绍，以前也是在这本书上看到解决方法后就再也没有忘记了。现在重新实现并记录一下，记录了从最低效的3重循环解决方法到最高效的线性时间解决方法及其中的优化考量。
继续阅读
合并排序是基于分治思想的：
1. 如果数组足够小，直接对数组进行排序。
2. 否则，把数组划分为两个子数组，分别进行合并排序，然后合并两个有序的子数组为有序数组。
进行合并操作的复杂度为O(n)，由于每次把数组分为2个子数组，需要进行lg(n)次合并，所以时间复杂度为O(n*lg(n))，。
每次合并都需要与两个子数组长度和 大小的数组，所以空间复杂度为O(n)。