一、引题
在一个N行M列的二维数组vec,每个元素位置放置一定数量的苹果,从底部开始往顶部走,每一步只能按 正前方、正前方左45度(如果左边还有位置)、正前方右45度(如果右边还有位置) 三种方式前进,起点可以是底部的任意一个位置,终点也可以是顶部的任意一个位置,求一条路径,使得按这条路径走过时能收集到最多的苹果。
分析
结果是要找出一条路径,使得按这条路径走时能收集到最多的苹果,这是找最优结果的问题。这样的路径当然没法一眼就看出来,可以随便画一条路径,但没法证明这条路径能得出最优结果。
那么能不能假设一个点vec[i][j],这个点是最优路径上的一个点。尽管现在还不能证明vec[i][j]肯定处于最优路径上,但我们就是假设它是(这是动态规划的分析的一个特点)!
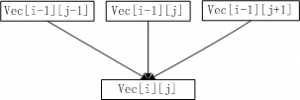
用cc[i][j]表示达到点vec[i][j]时能收集到的最多苹果数。按照题目的要求,如果vec[i][j]不是处于最底行,那么到达vec[i][j]最多有三种走法:
- 如果左上方还有位置,从vec[i-1][j-1]向右前方前进一步。
- 从vec[i-1][j]按正前方前进一步。
- 如果右上方还有位置,从vec[i-1][j+1]向左前方前进一步。
要在vec[i][j]收集到最多苹果,当然是从它的三个来源中选一个能收集到最多苹果的节点作为vec[i][j]在最优路径上的前一个节点。那么在vec[i][j]上收集到的苹果数为:
cc[i][j] = vec[i][j] + max{ cc[i-1][j-1] if j-1>=0, cc[i-1][j], cc[i-1][j+1] if j+1 < M } if i-1 >= 0